Closed range theorem

In the mathematical theory of Banach spaces, the closed range theorem gives necessary and sufficient conditions for a closed densely defined operator to have closed range. The theorem was proved by Stefan Banach in his 1932 Théorie des opérations linéaires.

Let X and Y be Banach spaces, T : D(X) → Y a closed linear operator whose domain D(X) is dense in X, and 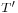$\scriptstyle{T'}$ its transpose. The theorem asserts that the following conditions are equivalent:

R(T), the range of T, is closed in Y
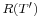$\scriptstyle{R(T')}$ , the range of 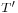$\scriptstyle{T'}$ , is closed in 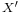$\scriptstyle{X'}$ , the dual of X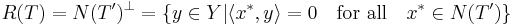
$R(T) = N(T')^\perp=\{y\in Y | \langle x^*,y\rangle = 0\quad {\text{for all}}\quad x^*\in N(T')\}$
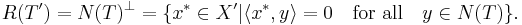
$R(T') = N(T)^\perp=\{x^*\in X' | \langle x^*,y\rangle = 0\quad {\text{for all}}\quad y\in N(T)\}.$

Several corollaries are immediate from the theorem. For instance, a densely defined closed operator T as above has R(T) = Y if and only if the transpose has a continuous inverse. Similarly, 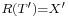$\scriptstyle{R(T') = X'}$ if and only if T has a continuous inverse.

References

Yosida, K. (1980), Functional Analysis, Grundlehren der Mathematischen Wissenschaften (Fundamental Principles of Mathematical Sciences), vol. 123 (6th ed.), Berlin, New York: Springer-Verlag .

‹The stub template below has been proposed for renaming to . See stub types for deletion to help reach a consensus on what to do.
Feel free to edit the template, but the template must not be blanked, and this notice must not be removed, until the discussion is closed. For more information, read the guide to deletion.›

Closed range theorem

See also

References